Zündkreisberechnung: Unterschied zwischen den Versionen
Gecko (Diskussion | Beiträge) |
Pyro (Diskussion | Beiträge) K (Online Zündkreisrechner eingefügt) |
||
| (14 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | ==Serien-/ | + | [[Bild:Reihenschaltung.gif|thumb|Reihenschaltung]] |
| − | + | ==Serien-/Reihenschaltung== | |
| + | ===Grundsätzliches=== | ||
| + | In einer Reihenschaltung (auch Serienschaltung genannt) werden die einzelnen [[Elektroanzünder]] hintereinander in einen Stromkreis eingesetzt (siehe Skizze). Dadurch ist die Stromstärke an jedem Punkt des [[Zündkreis]]es gleich groß. Der Vorteil dieser Schaltung ist, dass man den Gesamtwiderstand des Zündkreises einfach berechnen kann, und Fehler im Aufbau (vergessener Zünder, schlechter elektrischer Kontakt, defekter Zünder) sich durch messbare Unterschiede im Widerstand bemerkbar machen. Reihenschaltungen lassen sich dadurch vor Beginn eines Feuerwerks gut kontrollieren. Ein Nachteil der Schaltung liegt darin, dass alle Zünder in einem Zündkreis den gleichen Typ haben müssen (besser noch aus der gleichen Fertigungscharge stammen sollten). Denn ein einzelner früher auslösender Zünder unterbricht den kompletten Stromkreis, und die restlichen Zünder lösen dann nicht mehr aus. Weiterhin muss die Stromquelle (Akku, Kurbelzündmaschine,...) bei Zündkreisen mit vielen Zündern (und damit großem Gesamtwiderstand) eine ausreichend große Spannung bereitstellen können, um eine für die Zündung ausreichende Stromstärke zu erreichen. | ||
| − | + | ===Berechnung=== | |
| + | '''"Wie viele Zünder kann man in Reihe schalten?"''' | ||
| − | In einer Serien- oder Reihenschaltung ist die Stromstärke I an jeder Stelle eines [[Zündkreis|Zündkreises]] gleich groß und abhängig von der Spannung U der | + | Damit ein Elektroanzünder sicher auslöst, muss seine Ansprechstromstärke überschritten werden (0,6 A für A-Anzünder, 1,3 A für U-Anzünder, näheres unter dem Stichwort "[[Elektroanzünder]]"). Um mehrere Anzünder in Reihe auszulösen, sollte die Stromstärke über diesen Minimalwerten liegen, um die Fertigungstoleranzen der Anzünder auszugleichen. |
| + | |||
| + | In einer Serien- oder Reihenschaltung ist die Stromstärke I an jeder Stelle eines [[Zündkreis|Zündkreises]] gleich groß und abhängig von der Spannung U der Stromquelle (Akku, Kurbelzündmaschine, etc) sowie dem Gesamtwiderstand R des Zündkreises und wird durch das Ohmsche Gesetz beschrieben: | ||
R = U/I | R = U/I | ||
| Zeile 13: | Zeile 18: | ||
Die mögliche Anzahl der Zünder in einem Zündkreis ergibt sich aus | Die mögliche Anzahl der Zünder in einem Zündkreis ergibt sich aus | ||
| − | n=(U<sub>Zündquelle</sub>/I<sub>benötigt</sub> | + | n=(U<sub>Zündquelle</sub>/I<sub>benötigt</sub> - R<sub>Leitung</sub>)/R<sub>Anzünder</sub> |
| Zeile 21: | Zeile 26: | ||
* der Spannung, die die Zündquelle liefert -> U<sub>Zündquelle</sub> | * der Spannung, die die Zündquelle liefert -> U<sub>Zündquelle</sub> | ||
| − | + | ===Rechenbeispiel=== | |
| − | ===Rechenbeispiel | ||
Mit einem 12 V-Akku sollen mehrere A-Zünder in Reihe gezündet werden, die Stromstärke soll dabei mindestens 0,8 A betragen. Jeder Anzünder habe einen Widerstand von 2 Ω. | Mit einem 12 V-Akku sollen mehrere A-Zünder in Reihe gezündet werden, die Stromstärke soll dabei mindestens 0,8 A betragen. Jeder Anzünder habe einen Widerstand von 2 Ω. | ||
Die Zündleitung aus Kupfer habe einen Leitungsquerschnitt von 0,25 mm² und eine Länge von insgesamt 50 m (Achtung: Hin- und Rückleitung nötig). | Die Zündleitung aus Kupfer habe einen Leitungsquerschnitt von 0,25 mm² und eine Länge von insgesamt 50 m (Achtung: Hin- und Rückleitung nötig). | ||
| − | Die Zündleitung hat also einen Widerstand von 0, | + | Die Zündleitung hat also einen Widerstand von |
| + | R<sub>Leitung</sub>=(0,018 Ω mm<sup>2</sup>/m)/(0,25 mm<sup>2</sup>) * 50 m = '''3,6 Ohm''' | ||
(Formeln und Werte für andere Materialien unter dem Stichwort "[[Zündleitung]]"). | (Formeln und Werte für andere Materialien unter dem Stichwort "[[Zündleitung]]"). | ||
| − | Alle Werte in die Gleichung eingesetzt: | + | Alle Werte in die Gleichung eingesetzt, um die Anzahl der Zünder zu berechnen: |
| − | n= (12 V/0,8 A - 3,6 Ω) / 2 Ω = 11,4/2 = 5,7 | + | n= (12 V / 0,8 A - 3,6 Ω) / 2 Ω = 11,4 / 2 = '''5,7''' |
Man kann in diesem Fall bis zu 5 Zünder in Reihe schalten, ohne die Stromstärke von 0,8 A zu unterschreiten. | Man kann in diesem Fall bis zu 5 Zünder in Reihe schalten, ohne die Stromstärke von 0,8 A zu unterschreiten. | ||
| + | |||
| + | |||
| + | [[Bild:Parallelschaltung.gif|thumb|Parallelschaltung]] | ||
| + | ==Parallelschaltung== | ||
| + | ===Grundsätzliches=== | ||
| + | Bei der Parallelschaltung werden die einzelnen Zünder nicht hintereinander, sondern nebeneinander geschaltet. Das bedeutet, das jeder Zünder ohne den Umweg über einen weiteren Zünder direkt an der Zündquelle angeschlossen ist (siehe Skizze). Der Vorteil bei dieser Schaltung ist, das man mit einer sehr viel geringeren Zündspannung viele Zünder zünden kann. Neben der geringeren benötigten Zündspannung ist die Ausfallsicherheit bei einem parallel gezündeten Kreis erheblich größer, da ein defekter (oder z.B. abgerissener) Zünder nicht gleich Auswirkungen auf den gesamten Kreis hat. Dieses Argument fällt allerdings im Vergleich zur Reihenschaltung weg, wenn sowieso alle Zündkreise vor Beginn der Show kontrolliert werden. Ein Anwendungsfall, bei dem sich der Einsatz einer Parallel- oder gemischten Reihen- und Parallelschaltung nicht vermeiden lässt, ist der Einsatz mehrerer unterschiedlicher Zündertypen in einem Kreis. Da verschiedene Zünder unterschiedliche Ansprechstromstärken besitzen, würde bei unterschiedlichen Zündertypen der A-Zünder sehr viel früher auslösen und den Stromkreis unterbrechen, so das die U-Zünder nicht mehr auslösen könnte. | ||
| + | Diesen Vorteilen stehen jedoch einige gravierende Nachteile gegenüber, so dass diese Schaltungsart bei professionellen Feuerwerken nur in Sonderfällen zum Einsatz kommt. Das bedeutenste Manko der Parallelschaltung ist, dass sich die Kontrolle des Zündkreises äußerst schwierig gestaltet. Ein defekter oder falsch angeschlossener Zünder macht sich nämlich bei der Kontrolle mit einem [[Multimeter]] nur in einer äußerst geringen Änderung des Widerstandes bemerkbar. Eine solche geringe Abweichung kann jedoch auch durch den Übergangswiderstand an den Verbindungsstellen oder durch geringfügig abweichende Kabelquerschnitte zustande kommen, so das im Zweifel nicht eindeutig feststellbar ist ob es überhaupt ein Problem mit einem der Zünder gibt. | ||
| + | Zudem ist bei der Parallelschaltung alleine schon die Berechnung des Soll-Widerstandes (d.H. des Widerstandes den man bei der Messung erwartet) - zumindest bei unterschiedlichen Kabelstrecken bis zu den einzelnen Zündern - sehr aufwändig. Dies trägt zusätzlich zur Unsicherheit ob der Zündkreis funktionstüchtig ist, bei. | ||
| + | |||
| + | ===Berechnung=== | ||
| + | Zur Berechnung einer Parallelschaltung muss diese in unterschiedliche, kleinere Abschnitte aufgeteilt werden - und dies überall da, wo ein Zünder angeschlossen ist. Man beginnt die Berechnung an der Zündquelle. Der Widerstand beträgt hier: | ||
| + | R<sub>gesamt</sub> = R<sub>Leitung</sub> + R<sub>Verbleibender Zündkreis</sub> | ||
| + | Der Kabelwiderstand bis zur ersten Abzweigstelle kann (wie oben gezeigt) aus der Kabellänge, dem Querschnitt und dem Material berechnet werden, der Widerstand des verbleibenden Zündkreises muss jetzt durch die folgende Formel errechnet werden: | ||
| + | R<sub>Verbleibender Zündkreis</sub> = 1 / ( ( 1 / R<sub>Rechter Zweig</sub> ) + ( 1 / R<sub>Linker Zweig</sub> ) ) | ||
| + | Zumindest einer der beiden Zweige wird sich allerdings nicht einfach aus Kabelwiderstand plus Zünderwiderstand errechnen lassen, sondern wieder eine eigene Parallelschaltung darstellen (jedenfalls wenn mehr als zwei Zünder verwendet werden - was meist der Fall sein dürfte). Die gesamte Rechnung wird hier also (mit dem Ansatzpunkt der ersten Verzweigung statt der Zündquelle) von vorne los gehen und sich für jede Abzweigung in dieser Weise wiederholen. | ||
| + | Bei einem sonst einfach zu berechnenden Zündkreis mit 5 Verzweigungen ist man also ganz schnell bei 4 Einzelrechnungen - die jede für sich fehleranfällig ist, da sie nicht nur aus einer einfachen Additionen besteht. | ||
| + | |||
| + | [[Bild:Parallelschaltung.gif|thumb|Parallelschaltung]] | ||
| + | ===Rechenbeispiel=== | ||
| + | Das folgende Rechenbeispiel verdeutlicht dies, es bezieht sich auf die nebenstehende Skizze der Parallelschaltung. Der Einfachheit halber gehen wir davon aus, das die Widerstände der Kabel und Zünder bereits vorher durch eine entsprechende Rechnung (siehe oben) ermittelt wurden. Gegeben sind folgende Parameter: | ||
| + | *Der Kabelwiderstand zwischen der Zündquelle und dem ersten Abzweigpunkt beträgt 25 Ohm. | ||
| + | *Der Widerstand jedes einzelnen Zünderanschlusses (der waagerecht abzweigenden Kabel) inclusive dem angeschlossenen Zünder beträgt 5 Ohm. | ||
| + | *Der Kabelwiderstand zwischen zwei Anschlusspunkten (auch zwischen dem 4. und dem letzten Anschlusspunkt) beträgt 10 Ohm. | ||
| + | Dieser Zündkreis ist zwar sehr groß, kommt aber in der Praxis (dann jedoch meist als Reihenschaltung) bei großen Fronten nicht selten vor. | ||
| + | |||
| + | R<sub>Gesamt</sub> = R<sub>Zuleitung</sub> + R<sub>Rest 1</sub> | ||
| + | R<sub>Zuleitung</sub> = 25 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Rest 1</sub> = 1 / ( ( 1 / R<sub>Zünder 1</sub> ) + ( 1 / ( R<sub>Zwischenkabel 1-2</sub> + R<sub>Rest 2</sub> ) ) ) | ||
| + | R<sub>Zwischenkabel 1-2</sub> = 10 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Zünder 1</sub> = 5 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Rest 2</sub> = 1 / ( ( 1 / R<sub>Zünder 2</sub> ) + ( 1 / ( R<sub>Zwischenkabel 2-3</sub> + R<sub>Rest 3</sub> ) ) ) | ||
| + | R<sub>Zwischenkabel 2-3</sub> = 10 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Zünder 2</sub> = 5 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Rest 3</sub> = 1 / ( ( 1 / R<sub>Zünder 3</sub> ) + ( 1 / ( R<sub>Zwischenkabel 3-4</sub> + R<sub>Rest 4</sub> ) ) ) | ||
| + | R<sub>Zwischenkabel 3-4</sub> = 10 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Zünder 3</sub> = 5 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Rest 4</sub> = 1 / ( ( 1 / R<sub>Zünder 4</sub> ) + ( 1 / ( R<sub>Zwischenkabel 4-5</sub> + R<sub>Rest 5</sub> ) ) ) | ||
| + | R<sub>Zwischenkabel 4-5</sub> = 10 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Zünder 4</sub> = 5 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Rest 5</sub> = R<sub>Zünder 5</sub> = 5 Ohm <i>(gegeben)</i> | ||
| + | |||
| + | Jetzt kann man, von hinten beginnend, anfangen den Widerstand des Zündkreises auszurechnen (Ergebnisse fett): | ||
| + | |||
| + | R<sub>Rest 5</sub> = R<sub>Zünder 5</sub> = 5 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Zünder 4</sub> = 5 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Zwischenkabel 4-5</sub> = 10 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Rest 4</sub> = 1 / ( ( 1 / R<sub>Zünder 4</sub> ) + ( 1 / ( R<sub>Zwischenkabel 4-5</sub> + R<sub>Rest 5</sub> ) ) ) = <b>3,75 Ohm</b> | ||
| + | R<sub>Zünder 3</sub> = 5 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Zwischenkabel 3-4</sub> = 10 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Rest 3</sub> = 1 / ( ( 1 / R<sub>Zünder 3</sub> ) + ( 1 / ( R<sub>Zwischenkabel 3-4</sub> + R<sub>Rest 4</sub> ) ) ) = <b>3,6666 Ohm</b> | ||
| + | R<sub>Zünder 2</sub> = 5 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Zwischenkabel 2-3</sub> = 10 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Rest 2</sub> = 1 / ( ( 1 / R<sub>Zünder 2</sub> ) + ( 1 / ( R<sub>Zwischenkabel 2-3</sub> + R<sub>Rest 3</sub> ) ) ) = <b>3,6607 Ohm</b> | ||
| + | R<sub>Zünder 1</sub> = 5 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Zwischenkabel 1-2</sub> = 10 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Rest 1</sub> = 1 / ( ( 1 / R<sub>Zünder 1</sub> ) + ( 1 / ( R<sub>Zwischenkabel 1-2</sub> + R<sub>Rest 2</sub> ) ) ) = <b>3,6602 Ohm</b> | ||
| + | |||
| + | Zu diesem Ergebnis wird die Zuleitung wie bei einer normalen Reihenschaltung addiert: | ||
| + | |||
| + | R<sub>Zuleitung</sub> = 25 Ohm <i>(gegeben)</i> | ||
| + | R<sub>Gesamt</sub> = R<sub>Zuleitung</sub> + R<sub>Rest 1</sub> = <b>28,6602 Ohm</b> | ||
| + | |||
| + | Die genaue Angabe der Werte soll hier nur zeigen, wie gering die Abweichung bei jedem einzelnen Zünder der hinzukommt wird. Fällt jetzt zum Beispiel Zünder 5 komplett aus, wäre die obere Rechnung die selbe - allerdings mit 4 statt mit 5 Zündern, der letzte Rechenschritt im ersten Rechenblock (also nicht die Addition der Zuleitung) würde komplett wegfallen, und wir hätten (nach Addition des Zuleitungswiderstandes) einen zu erwartenden Widerstand von 28,6607 Ohm statt 28,6602 Ohm - ein Unterschied der in der Praxis nicht messbar ist. Der Fehler des letzten Zünders würde hier also bei einer Messung an der Zündquelle unbemerkt bleiben. | ||
| + | |||
| + | ==Weblinks== | ||
| + | *[http://fw.fw.eu/ Online Zündkreisrechner] | ||
[[Kategorie:Praxis]] | [[Kategorie:Praxis]] | ||
[[Kategorie:Technik]] | [[Kategorie:Technik]] | ||
Aktuelle Version vom 27. Juni 2016, 18:27 Uhr
Inhaltsverzeichnis
[Verbergen]Serien-/Reihenschaltung
Grundsätzliches
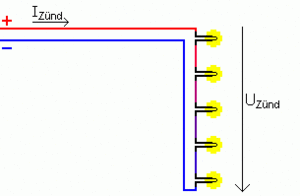
In einer Reihenschaltung (auch Serienschaltung genannt) werden die einzelnen Elektroanzünder hintereinander in einen Stromkreis eingesetzt (siehe Skizze). Dadurch ist die Stromstärke an jedem Punkt des Zündkreises gleich groß. Der Vorteil dieser Schaltung ist, dass man den Gesamtwiderstand des Zündkreises einfach berechnen kann, und Fehler im Aufbau (vergessener Zünder, schlechter elektrischer Kontakt, defekter Zünder) sich durch messbare Unterschiede im Widerstand bemerkbar machen. Reihenschaltungen lassen sich dadurch vor Beginn eines Feuerwerks gut kontrollieren. Ein Nachteil der Schaltung liegt darin, dass alle Zünder in einem Zündkreis den gleichen Typ haben müssen (besser noch aus der gleichen Fertigungscharge stammen sollten). Denn ein einzelner früher auslösender Zünder unterbricht den kompletten Stromkreis, und die restlichen Zünder lösen dann nicht mehr aus. Weiterhin muss die Stromquelle (Akku, Kurbelzündmaschine,...) bei Zündkreisen mit vielen Zündern (und damit großem Gesamtwiderstand) eine ausreichend große Spannung bereitstellen können, um eine für die Zündung ausreichende Stromstärke zu erreichen.
Berechnung
"Wie viele Zünder kann man in Reihe schalten?"
Damit ein Elektroanzünder sicher auslöst, muss seine Ansprechstromstärke überschritten werden (0,6 A für A-Anzünder, 1,3 A für U-Anzünder, näheres unter dem Stichwort "Elektroanzünder"). Um mehrere Anzünder in Reihe auszulösen, sollte die Stromstärke über diesen Minimalwerten liegen, um die Fertigungstoleranzen der Anzünder auszugleichen.
In einer Serien- oder Reihenschaltung ist die Stromstärke I an jeder Stelle eines Zündkreises gleich groß und abhängig von der Spannung U der Stromquelle (Akku, Kurbelzündmaschine, etc) sowie dem Gesamtwiderstand R des Zündkreises und wird durch das Ohmsche Gesetz beschrieben:
R = U/I
Bei vorgegebener Spannung der Zündquelle und bekannter benötigter Stromstärke läßt sich damit der maximal mögliche Gesamtwiderstand berechnen.
Der Gesamtwiderstand des Zündkreises setzt sich (unter Vernachlässigung der Übergangswiderstände) aus den Widerständen der einzelnen Anzünder (Anzahl n) und dem Widerstand der Zündleitung zusammen:
Rgesamt=RLeitung + n*RAnzünder
Die mögliche Anzahl der Zünder in einem Zündkreis ergibt sich aus
n=(UZündquelle/Ibenötigt - RLeitung)/RAnzünder
Die Antwort auf die oben gestellte Frage ist also abhängig von
- der Art des Anzünders (A oder U, Widerstand von Zündpille und Zünderdraht) -> RAnzünder, Ibenötigt
- der Art (Material, Leitungsquerschnitt) und Länge der Zündleitung -> RLeitung
- der Spannung, die die Zündquelle liefert -> UZündquelle
Rechenbeispiel
Mit einem 12 V-Akku sollen mehrere A-Zünder in Reihe gezündet werden, die Stromstärke soll dabei mindestens 0,8 A betragen. Jeder Anzünder habe einen Widerstand von 2 Ω.
Die Zündleitung aus Kupfer habe einen Leitungsquerschnitt von 0,25 mm² und eine Länge von insgesamt 50 m (Achtung: Hin- und Rückleitung nötig). Die Zündleitung hat also einen Widerstand von
RLeitung=(0,018 Ω mm2/m)/(0,25 mm2) * 50 m = 3,6 Ohm
(Formeln und Werte für andere Materialien unter dem Stichwort "Zündleitung").
Alle Werte in die Gleichung eingesetzt, um die Anzahl der Zünder zu berechnen:
n= (12 V / 0,8 A - 3,6 Ω) / 2 Ω = 11,4 / 2 = 5,7
Man kann in diesem Fall bis zu 5 Zünder in Reihe schalten, ohne die Stromstärke von 0,8 A zu unterschreiten.
Parallelschaltung
Grundsätzliches
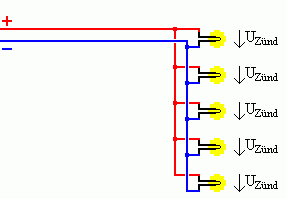
Bei der Parallelschaltung werden die einzelnen Zünder nicht hintereinander, sondern nebeneinander geschaltet. Das bedeutet, das jeder Zünder ohne den Umweg über einen weiteren Zünder direkt an der Zündquelle angeschlossen ist (siehe Skizze). Der Vorteil bei dieser Schaltung ist, das man mit einer sehr viel geringeren Zündspannung viele Zünder zünden kann. Neben der geringeren benötigten Zündspannung ist die Ausfallsicherheit bei einem parallel gezündeten Kreis erheblich größer, da ein defekter (oder z.B. abgerissener) Zünder nicht gleich Auswirkungen auf den gesamten Kreis hat. Dieses Argument fällt allerdings im Vergleich zur Reihenschaltung weg, wenn sowieso alle Zündkreise vor Beginn der Show kontrolliert werden. Ein Anwendungsfall, bei dem sich der Einsatz einer Parallel- oder gemischten Reihen- und Parallelschaltung nicht vermeiden lässt, ist der Einsatz mehrerer unterschiedlicher Zündertypen in einem Kreis. Da verschiedene Zünder unterschiedliche Ansprechstromstärken besitzen, würde bei unterschiedlichen Zündertypen der A-Zünder sehr viel früher auslösen und den Stromkreis unterbrechen, so das die U-Zünder nicht mehr auslösen könnte. Diesen Vorteilen stehen jedoch einige gravierende Nachteile gegenüber, so dass diese Schaltungsart bei professionellen Feuerwerken nur in Sonderfällen zum Einsatz kommt. Das bedeutenste Manko der Parallelschaltung ist, dass sich die Kontrolle des Zündkreises äußerst schwierig gestaltet. Ein defekter oder falsch angeschlossener Zünder macht sich nämlich bei der Kontrolle mit einem Multimeter nur in einer äußerst geringen Änderung des Widerstandes bemerkbar. Eine solche geringe Abweichung kann jedoch auch durch den Übergangswiderstand an den Verbindungsstellen oder durch geringfügig abweichende Kabelquerschnitte zustande kommen, so das im Zweifel nicht eindeutig feststellbar ist ob es überhaupt ein Problem mit einem der Zünder gibt. Zudem ist bei der Parallelschaltung alleine schon die Berechnung des Soll-Widerstandes (d.H. des Widerstandes den man bei der Messung erwartet) - zumindest bei unterschiedlichen Kabelstrecken bis zu den einzelnen Zündern - sehr aufwändig. Dies trägt zusätzlich zur Unsicherheit ob der Zündkreis funktionstüchtig ist, bei.
Berechnung
Zur Berechnung einer Parallelschaltung muss diese in unterschiedliche, kleinere Abschnitte aufgeteilt werden - und dies überall da, wo ein Zünder angeschlossen ist. Man beginnt die Berechnung an der Zündquelle. Der Widerstand beträgt hier:
Rgesamt = RLeitung + RVerbleibender Zündkreis
Der Kabelwiderstand bis zur ersten Abzweigstelle kann (wie oben gezeigt) aus der Kabellänge, dem Querschnitt und dem Material berechnet werden, der Widerstand des verbleibenden Zündkreises muss jetzt durch die folgende Formel errechnet werden:
RVerbleibender Zündkreis = 1 / ( ( 1 / RRechter Zweig ) + ( 1 / RLinker Zweig ) )
Zumindest einer der beiden Zweige wird sich allerdings nicht einfach aus Kabelwiderstand plus Zünderwiderstand errechnen lassen, sondern wieder eine eigene Parallelschaltung darstellen (jedenfalls wenn mehr als zwei Zünder verwendet werden - was meist der Fall sein dürfte). Die gesamte Rechnung wird hier also (mit dem Ansatzpunkt der ersten Verzweigung statt der Zündquelle) von vorne los gehen und sich für jede Abzweigung in dieser Weise wiederholen. Bei einem sonst einfach zu berechnenden Zündkreis mit 5 Verzweigungen ist man also ganz schnell bei 4 Einzelrechnungen - die jede für sich fehleranfällig ist, da sie nicht nur aus einer einfachen Additionen besteht.
Rechenbeispiel
Das folgende Rechenbeispiel verdeutlicht dies, es bezieht sich auf die nebenstehende Skizze der Parallelschaltung. Der Einfachheit halber gehen wir davon aus, das die Widerstände der Kabel und Zünder bereits vorher durch eine entsprechende Rechnung (siehe oben) ermittelt wurden. Gegeben sind folgende Parameter:
- Der Kabelwiderstand zwischen der Zündquelle und dem ersten Abzweigpunkt beträgt 25 Ohm.
- Der Widerstand jedes einzelnen Zünderanschlusses (der waagerecht abzweigenden Kabel) inclusive dem angeschlossenen Zünder beträgt 5 Ohm.
- Der Kabelwiderstand zwischen zwei Anschlusspunkten (auch zwischen dem 4. und dem letzten Anschlusspunkt) beträgt 10 Ohm.
Dieser Zündkreis ist zwar sehr groß, kommt aber in der Praxis (dann jedoch meist als Reihenschaltung) bei großen Fronten nicht selten vor.
RGesamt = RZuleitung + RRest 1 RZuleitung = 25 Ohm (gegeben) RRest 1 = 1 / ( ( 1 / RZünder 1 ) + ( 1 / ( RZwischenkabel 1-2 + RRest 2 ) ) ) RZwischenkabel 1-2 = 10 Ohm (gegeben) RZünder 1 = 5 Ohm (gegeben) RRest 2 = 1 / ( ( 1 / RZünder 2 ) + ( 1 / ( RZwischenkabel 2-3 + RRest 3 ) ) ) RZwischenkabel 2-3 = 10 Ohm (gegeben) RZünder 2 = 5 Ohm (gegeben) RRest 3 = 1 / ( ( 1 / RZünder 3 ) + ( 1 / ( RZwischenkabel 3-4 + RRest 4 ) ) ) RZwischenkabel 3-4 = 10 Ohm (gegeben) RZünder 3 = 5 Ohm (gegeben) RRest 4 = 1 / ( ( 1 / RZünder 4 ) + ( 1 / ( RZwischenkabel 4-5 + RRest 5 ) ) ) RZwischenkabel 4-5 = 10 Ohm (gegeben) RZünder 4 = 5 Ohm (gegeben) RRest 5 = RZünder 5 = 5 Ohm (gegeben)
Jetzt kann man, von hinten beginnend, anfangen den Widerstand des Zündkreises auszurechnen (Ergebnisse fett):
RRest 5 = RZünder 5 = 5 Ohm (gegeben) RZünder 4 = 5 Ohm (gegeben) RZwischenkabel 4-5 = 10 Ohm (gegeben) RRest 4 = 1 / ( ( 1 / RZünder 4 ) + ( 1 / ( RZwischenkabel 4-5 + RRest 5 ) ) ) = 3,75 Ohm RZünder 3 = 5 Ohm (gegeben) RZwischenkabel 3-4 = 10 Ohm (gegeben) RRest 3 = 1 / ( ( 1 / RZünder 3 ) + ( 1 / ( RZwischenkabel 3-4 + RRest 4 ) ) ) = 3,6666 Ohm RZünder 2 = 5 Ohm (gegeben) RZwischenkabel 2-3 = 10 Ohm (gegeben) RRest 2 = 1 / ( ( 1 / RZünder 2 ) + ( 1 / ( RZwischenkabel 2-3 + RRest 3 ) ) ) = 3,6607 Ohm RZünder 1 = 5 Ohm (gegeben) RZwischenkabel 1-2 = 10 Ohm (gegeben) RRest 1 = 1 / ( ( 1 / RZünder 1 ) + ( 1 / ( RZwischenkabel 1-2 + RRest 2 ) ) ) = 3,6602 Ohm
Zu diesem Ergebnis wird die Zuleitung wie bei einer normalen Reihenschaltung addiert:
RZuleitung = 25 Ohm (gegeben) RGesamt = RZuleitung + RRest 1 = 28,6602 Ohm
Die genaue Angabe der Werte soll hier nur zeigen, wie gering die Abweichung bei jedem einzelnen Zünder der hinzukommt wird. Fällt jetzt zum Beispiel Zünder 5 komplett aus, wäre die obere Rechnung die selbe - allerdings mit 4 statt mit 5 Zündern, der letzte Rechenschritt im ersten Rechenblock (also nicht die Addition der Zuleitung) würde komplett wegfallen, und wir hätten (nach Addition des Zuleitungswiderstandes) einen zu erwartenden Widerstand von 28,6607 Ohm statt 28,6602 Ohm - ein Unterschied der in der Praxis nicht messbar ist. Der Fehler des letzten Zünders würde hier also bei einer Messung an der Zündquelle unbemerkt bleiben.