Flugbahn

Flugbahn

Weg, den ein aufsteigender Feuerwerkskörper (Bombe, Rakete, etc.) nach der Zündung hinter sich bringt.

Bedingt durch die Schwerkraft und weitere Kräfte, die eine seitliche Abdrift bewirken, ist die Flugbahn auch bei senkrechtem Abschuss der Feuerwerkskörper mehr oder weniger parabelförmig.

Physikalische Beschreibung der Flugbahn

Pyrotechnische Gegenstände ohne Eigenantrieb

Physikalische Kräfte, die die Flugbahn einer Kugelbombe nach dem Abschuss beeinflussen (ohne Wind).

Hierunter fallen z.B. Kugelbomben, Zylinderbomben und Bombetten.

Die Flugbahn einer Kugelbombe wird bestimmt durch ihre Geschwindigkeit und Richtung beim Verlassen des Abschussrohres sowie die Summe der physikalischen Kräfte, die danach auf sie wirken.

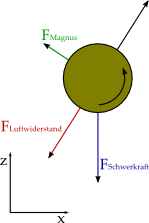
Dazu gehören die Schwerkraft, der Luftwiderstand der Kugelbombe, die Magnuskraft, die durch die Rotation der fliegenden Kugelbombe entsteht, und die Kraft, die der Wind auf die Bombe ausübt.

Bei korrekter Funktion des pyrotechnischen Gegenstands wird die Zerlegerladung nahe des Zenits der Flugbahn gezündet, so dass seine Flugbahn dort endet (die Bewegung der Bombenschalen-Reste soll hier nicht weiter betrachtet werden).

Schwerkraft: Durch die Wirkung der Schwerkraft entsteht die parabelförmige "Grundform" der Flugbahn; sie wirkt stets in vertikaler Richtung auf die Kugelbombe. Die Gravitationskraft berechnet sich aus

FSchwerkraft = -mptG * g,

wobei mptG die Masse des pyrotechnischen Gegenstands (ptG) und g die Erdbeschleunigung ist.

Luftwiderstand: Da die Kugelbombe eine hohe Anfangsgeschwindigkeit hat, muss ihr Luftwiderstand mitberücksichtigt werden. Der Luftwiderstand wirkt stets dem Geschwindigkeitsvektor entgegengesetzt, und ist proportional zum Quadrat der Geschwindigkeit der Kugelbombe. Durch den Luftwiderstand wird zum einen die Steighöhe der Bombe verkürzt, zum anderen wird die horizontale Geschwindigkeit (bei gewinkeltem Abschuss, oder durch andere Kräfte verursacht) verringert, was zu einer Asymmetrie der Flugparabel führt (der "absteigende Ast" der Parabel ist steiler als der "aufsteigende Ast"). Die aus dem Luftwiderstand resultierende Kraft ist

FLuftwiderstand = 1/2 * cw * ρLuft * vptG2 * AptG,

wobei cw der Luftwiderstandsbeiwert ist (für Kugeln ein Wert von etwa 0,4 bis 0,5). ρLuft steht für die Dichte der Luft, vptG ist die Geschwindigkeit und AptG die Querschnittsfläche der Kugelbombe .

Die Flugbahn, die sich aus dem gemeinsamen Wirken von Schwerkraft und Luftwiderstand ergibt, nennt man "ballistische Kurve".

Magnuskraft: Die Kugelbombe wird beim Abschuss in Rotation versetzt (durch leicht unterschiedliche Drücke beim Vorbeiströmen der heißen Explosionsgase an der Kugelbombe, die i.d.R. auch nicht perfekt rund ist). Die Rotation der Kugelbombe während des Fluges führt dazu, dass auch eine dünne Schicht der Luft direkt an der Oberfläche der Bombe in Rotation versetzt wird. Gleichzeitig bewegt sich die Kugelbombe durch die Luft, wodurch die Bombe von der umgebenden Luft umströmt wird. An der Seite der Kugelbombe, wo die Strömungsrichtung der mitrotierenden Luft derjenigen der Umgebungsluft entgegengesetzt ist, entsteht ein höherer Druck als auf der entgegengesetzten Seite. Das führt zu einer Kraft, die senkrecht zur Strömungsrichtung der Luft auf die Kugelbombe wirkt:

FMagnus = 1/2 * ck * ρLuft * vptG2 * AptG * (ω * dptG / vptG)

Dabei steht ck für den Beiwert der Magnuskraft (ca. 0,45 für eine rauhe Kugeloberfläche), ω für die Winkelgeschwindigkeit der Drehung und dptG für den Durchmesser der Kugelbombe.

Die Magnuskraft ist umso größer, je schneller die Bombe fliegt und um ihre Achse rotiert. Die Richtung der Magnuskraft ist abhängig von der Lage der Rotationsachse; die größte seitliche Abdrift aufgrund der Magnuskraft ergibt sich, wenn die Rotationsachse senkrecht zur Flugrichtung steht.

Windkraft: Wind führt zu einer Beschleunigung in horizontaler Richtung. Beschleunigung ist hier im physikalischen Sinn zu verstehen: fliegt die Bombe gegen den Wind, wird sie vom Wind abgebremst (negative Beschleunigung). Die Windgeschwindigkeit ist i.d.R. nicht konstant, sondern nimmt mit der Höhe zu. Anders formuliert: der Wind wird von der Bodenoberfläche gebremst. Je rauher die Oberfläche ist (Bäume, Gebäude), desto stärker ist diese Abschwächung, und desto größer ist der Unterschied der Windgeschwindigkeit am Boden und in der Höhe.

Die Kraft, die der Wind auf die Kugelbombe ausübt, ist also abhängig von der Höhe, in der sich die Kugelbombe befindet:

FWind = 1/2 * cw * ρLuft * vrel(z)2 * AptG

vrel ist die relative Anströmgeschwindigkeit, die sich aus Windgeschwindigkeit und Fluggeschwindigkeit der Bombe ergibt (als Funktion der Höhe z).


Aus diesen Kräften ergibt sich für die Bewegungsgleichung der Kugelbombe ein Differentialgleichungssystem, das numerisch gelöst werden muss:

F ges = mptG * aptG = d2s / d t2

wobei aptG die Beschleunigung, s(x,y,z) ein Ort auf der Bahnkurve, t die Zeit und Fges die Summe der wirksamen Kräfte ist (Beschleunigung und Kraft sind Vektoren). d steht für den Differentialoperator.



Pyrotechnische Gegenstände mit Eigenantrieb

Darunter fallen in erster Linie Raketen, auch steigende Kronen.

Der Eigenantrieb von Raketen beruht auf dem Rückstoßprinzip: die bei der Verbrennung des Treibsatzes entstehenden Gase (Masse) werden durch die Düse ausgestoßen, und die Rakete wird dadurch in die Gegenrichtung beschleunigt.

Mit Hilfe der Impulserhaltung läßt sich das so formulieren: d (mRakete*vRakete) / dt = - vGas * d(mRakete)/dt

m steht für die Masse, v für Geschwindigkeit und t für die Zeit.

Dazu kommen als äußere Kräfte noch die Gravitationskraft, der Luftwiderstand und evtl. die Windkraft.

Berücksichtigt man die Gravitation in der Raketengleichung, erhält man für die Geschwindigkeitsänderung einer senkrecht fliegenden Rakete folgende Gleichung:

mRakete * d (vRakete)/dt = -(vrel) * dmRakete / dt - mRakete*g

Dabei steht vrel = vGas + vRakete für die Ausströmgeschwindigkeit des Gases relativ zur Rakete und g für die Erdbeschleunigung.

Durch Integration ergibt sich als Geschwindigkeit der Rakete:

vRakete(t1) = vRakete(t0) + vrel * ln(mRakete(t0) / mRakete(t1)) - g * (t1 - t0)

Um die Flugbahn z(t) zu erhalten, muss diese Gleichung nochmals integriert werden.

Nachdem der Treibsatz abgebrannt ist, wird die Rakete zum Gegenstand ohne Eigenantrieb; die Flugbahn wird ab diesem Punkt von den gleichen Kräften beeinflusst, die oben für die Kugelbombe erläutert sind.

Literatur

D. Eckhardt, H. Andre (2000): Erkenntnisse und Schlussfolgerungen aus der Untersuchung eines Unfalles mit einer Großfeuerwerksbombe. SprengInfo 23(3), S. 15-23.

Weblinks

Abgerufen von „https://www.feuerwerk.net/wiki/index.php?title=Flugbahn&oldid=6407“